This page provides a brief overview of my Master’s thesis written at RWTH Aachen. The full Thesis is available as pdf and the code is accessible on my GitHub.
Motivation
Efficient evaluation of prices and sensitivities is an integral part of computational finance. While Monte Carlo methods provide high modeling flexibility, their computational cost severely limits their applicability in real-time settings, particularly for higher-order Greeks. Neural surrogate models offer a promising alternative, but their training typically relies on value-based objectives that underutilize derivative information, which limits both attainable accuracy and training efficiency.
Sobolev training extends classical regression by incorporating derivative supervision, leading to significant improvements in sample efficiency and generalization. However, naive extensions to second- and higher-order derivatives are computationally infeasible due to the quadratic and cubic growth of Hessians and higher-order derivative tensors. In this work, we show how randomized numerical linear algebra techniques can be combined with algorithmic differentiation to enable efficient directional higher-order supervision, allowing neural surrogates to learn prices and Greeks accurately in high-dimensional settings.
Sobolev Training
Let \(f: \mathbb{R}^d \rightarrow \mathbb{R}\) denote a (pricing) function and \(\hat{f}_\theta\) a neural surrogate parameterized by \( \theta \). Standard regression minimizes a value-based loss \[
\mathcal{L}_0(\theta)=\mathbb{E}_x\left[\left\|\hat{f}_\theta(x)-f(x)\right\|^2\right] .
\]
Sobolev Training incorporates derivatives of the function with respect to the inputs:
\[
\mathcal{L}_{\text {Sob }}(\theta)=\sum_{i=0}^n \lambda_i \mathbb{E}_x\left[\left\|\nabla_x^i \hat{f}_\theta(x)-\nabla_x^i f(x)\right\|^2\right] .
\]
In quantitative finance, this idea is known as Differential Machine Learning (DML). Even including first-order terms can lead to dramatic improvement in sample efficiency and generalization. However, extending this idea to second- and higher-order derivatives is problematic. The Hessian contains \(O\left(d^2\right)\) entries and third derivatives scale as \(O\left(d^3\right)\). For realistic pricing problems large input dimension, full supervision quickly becomes infeasible.
Directional Sobolev Training
A key observation is that in many financial models, curvature concentrates in a low-dimensional subspace. Let \[H_f(x)=\nabla_x^2 f(x) \in \mathbb{R}^{d \times d}\] denote the Hessian at position \(x\). Its eigenspectrum often decays rapidly, i.e. most curvature lives in a small subspace. This motivates replacing full Hessian supervision by directional curvature supervision. Given a small set of directions \(\left\{u_i\right\}_{i=1}^k \subset \mathbb{R}^d\), we define the second-order directional Sobolev loss
\[
\mathcal{L}_2(\theta ; x)=\frac{1}{k} \sum_{i=1}^k\left\|H_{\hat{f}_\theta}(x) u_i-H_f(x) u_i\right\|^2 .
\]
Crucially, Hessian-vector products (HVPs)
\[
H_f(x) u=\nabla_x^2 f(x) u
\]
can be computed efficiently via algorithmic differentiation at roughly the cost of a gradient evaluation, using the classical Pearlmutter trick. This reduces the computational cost from forming a dense \(d^2\) matrix to evaluating only \(k\) matrix-vector products, with \(k \ll d\).
The central challenge now becomes selecting the most informative directions for supervision.
Randomized Hessian Sketching
Rather than selecting directions heuristically or at random, we use tools from randomized numerical linear algebra to extract curvature-aware directions from the Hessian operator. For a batch of inputs \(\left\{x_b\right\}_{b=1}^m\) let
\[
\bar{H}_f=\frac{1}{m} \sum_{b=1}^m \nabla_x^2 f\left(x_b\right)
\]
denote the batch-averaged Hessian. Our goal is to approximate its dominant eigenspace in a matrix-free manner without explicitly forming any full Hessians.
We draw a random Gaussian test matrix \(\Omega \in \mathbb{R}^{d \times s}\) and compute the sketch
\[
Y=\bar{H}_f \Omega = \frac{1}{m} \sum_{b=1}^m H_f\left(x_b\right) \Omega,
\]
where each multiplication is realized using HVPs. We then compute an orthonormal basis \(Q=\operatorname{orth}(Y)\), and construct a compressed operator \(B=Q^{\top}\bar{H}_f \) by again evaluating HVPs. This is possible because the Hessians are symmetric and therefore \(Q^{\top} H_f\left(x_b\right)=\left(H_f\left(x_b\right)^{\top} Q\right)^{\top}=\left(H_f\left(x_b\right) Q\right)^{\top}\). Stacking the transposed HVPs row-wise yields the desired matrix \(B \in \mathbb{R}^{s \times d}\).
Performing a small SVD on \(B\) yields approximate dominant eigenvectors of the Hessian. These vectors form our curvature-aware supervision directions.
This procedure is a matrix-free adaptation of the randomized SVD algorithm of Halko et al., and apart from a small factoization its total cost scales as \[
O(k \cdot \operatorname{cost}(\mathrm{HVP})),
\] making it viable even for high-dimensional pricing models.
Third-Order Directional Supervision
The third derivative of a pricing function \(f: \mathbb{R}^d \rightarrow \mathbb{R}\) is a symmetric tensor
\[
T_f(x)=\nabla_x^3 f(x) \in \mathbb{R}^{d \times d \times d},
\]
whose size scales cubically in dimension. Direct supervision is therefore infeasible. However, just as in the second-order case, we can avoid materializing this tensor by exploiting directional derivative products. Using nested algorithmic differentiation, we can efficiently compute tensor-vector-vector products (TVVPs) of the form
\[
T_f(x)[\cdot, u, v]=\partial_v\left(H_f(x) u\right),
\]
which describe how the Hessian-vector product changes along direction \(v\). This allows us to probe thirdorder structure directionally, without ever forming the full tensor. The key challenge is again direction selection.
We start from a small set of sketcg directions \(\left\{u_i\right\}_{i=1}^s \subset \mathbb{R}^d\), chosen as dominant second-order curvature directions, plus a few random exploration directions.
Using these vectors, we probe the third-order tensor using all direction pairs and compute the batch-averaged TVVPs
\[
y_{i, j}=\frac{1}{m} \sum_{b=1}^m T_f\left(x_b\right)\left[\cdot, u_i, u_j\right] \in \mathbb{R}^d .
\]
Stacking these vectors produces the sketch
\[
Y=\frac{1}{m} \sum_{b=1}^m T_f^{(1)}\left(x_b\right) \Omega, \quad \Omega=\left\{\operatorname{vec}\left(u_i \otimes u_j\right)\right\}_{i, j} ,
\]
where \( T_f^{(1)}\left(x_b\right) \) is the mode-one unfolding of the third derivative tensor.
This sketch approximates the dominant left singular subspace of the unfolded third-order operator. From this sketch, we extract a small number of informative directions by ranking them according to the magnitude of their third-order contractions
\[
M(q)=\mathbb{E}_x\left[\left\|T_f(x)[\cdot, q, q]\right\|^2\right]
\]
and truncating. The resulting directions identify where curvature changes most strongly and are used for directional third-order supervision.
Adaptive Loss Balancing
Monte Carlo estimates of higher-order derivatives can be extremely noisy, particularly for second- and thirdorder terms. Blindly supervising these derivatives often degrades overall performance and can destabilize training, especially in high-dimensional stochastic models.
To address this, we adopt uncertainty-based loss weighting, following the probabilistic formulation introduced by Kendall et al. (2018) for multi-task learning. Each derivative order is assigned a learnable uncertainty parameter \(s_i\), yielding the total loss
\[
L_{\text {total }}(\theta ; x)=\sum_{i=0}^3\left(\frac{1}{2} \exp \left(-s_i\right) \lambda_i^{\text {base }} L_i(\theta ; x)+\frac{1}{2} s_i\right),
\]
where \(\lambda_i^{\text {base }}\) provides structural normalization (scale/order preferences), while \(\exp \left(-s_i\right)\) adapts to noise/difficulty during training.
This formulation arises naturally from a maximum-likelihood perspective, where each task is modeled as a Gaussian observation with unknown noise variance. During training, the network automatically learns which derivative orders are reliable and downweights those dominated by Monte Carlo noise. In practice, this mechanism proves essential for stabilizing higher-order supervision.
Results
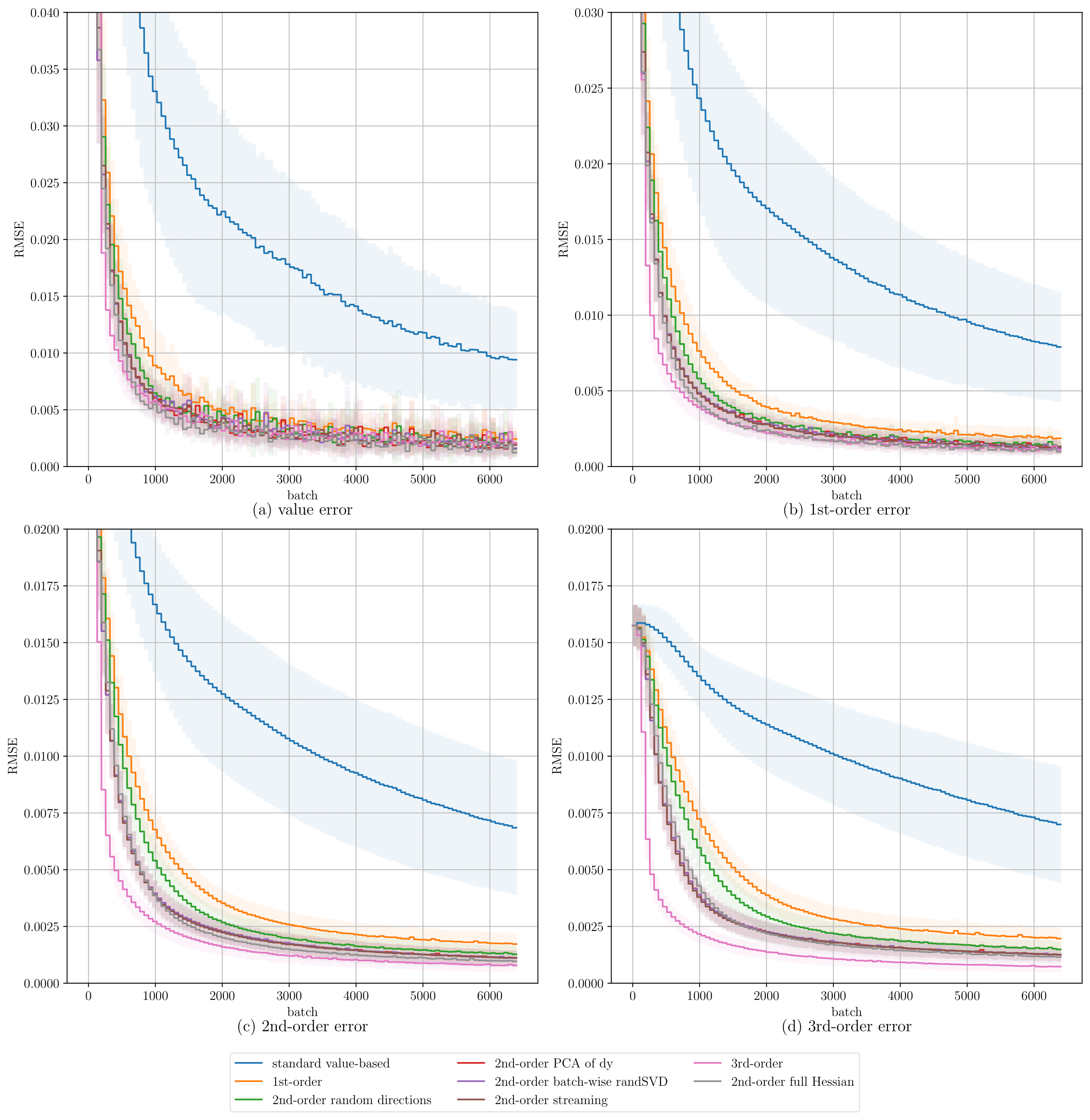
We first consider an analytic implementation of a Bachelier basket call option, where exact derivatives are available. This setting isolates algorithmic effects from Monte Carlo noise and provides a clean comparison of different training strategies. As shown in Figure 1, incorporating first-order derivative supervision already leads to a large improvement in both convergence speed and accuracy. Adding directional second-order supervision yields further gains. Randomized Hessian sketching converges faster and achieves lower errors than random-direction baselines, while matching the performance of full Hessian supervision at a fraction of the computational cost. Third-order supervision further improves higher-order accuracy and slightly accelerates convergence, confirming that higher-order information can be exploited effectively.
Fig. 1: Test-set RMSEs over training batches. Curves show mean RMSE across 10 random seeds with shaded standard deviations. Panels show errors in the predicted values and the learned derivatives.
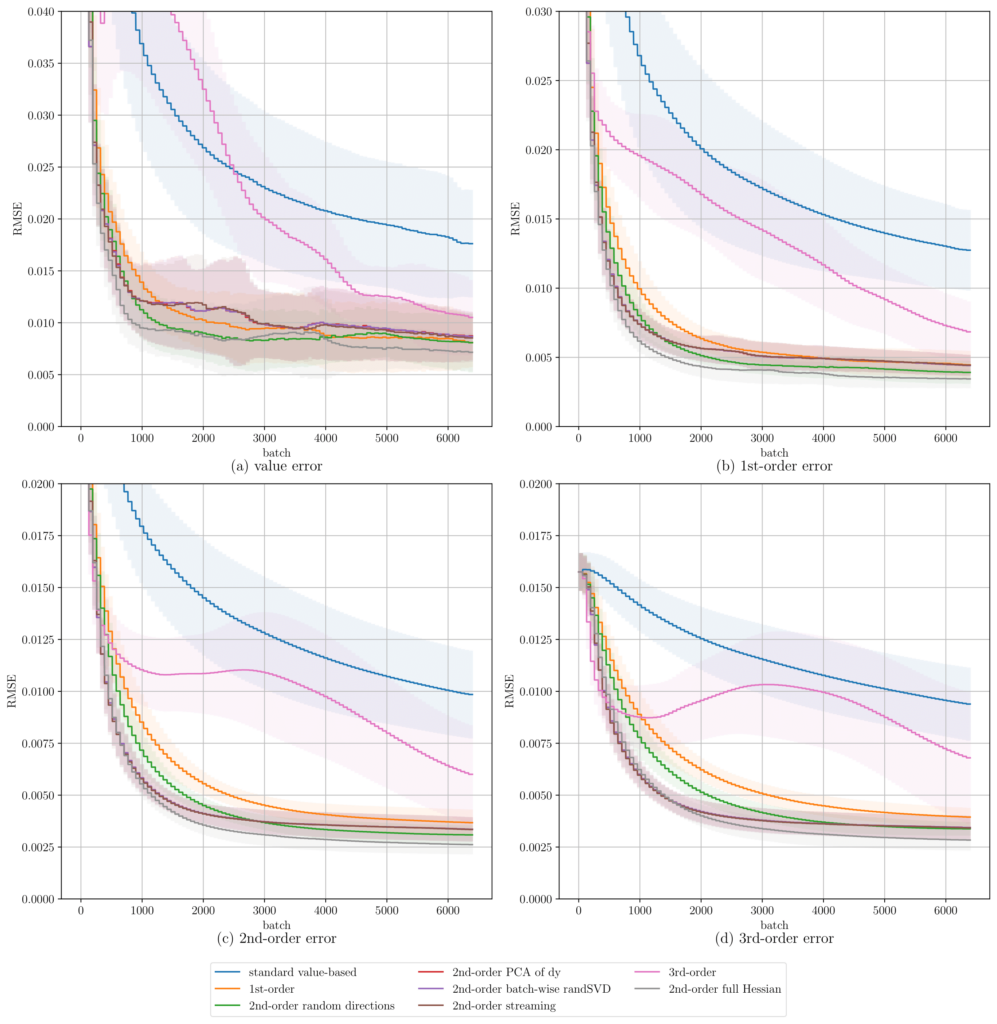
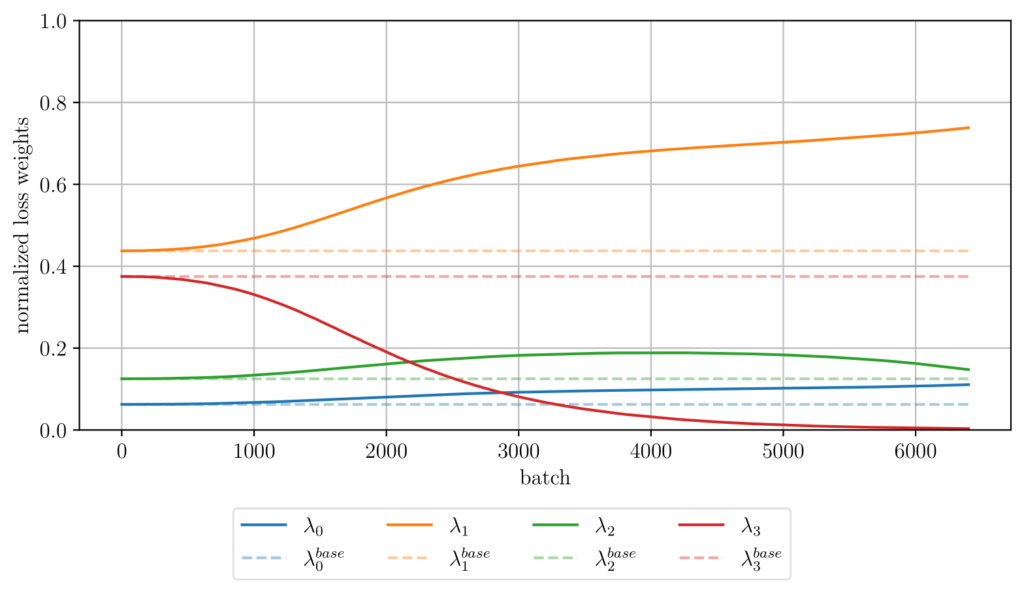
We next consider a Monte Carlo approximation of the same Bachelier basket model, using pathwise derivatives from single simulation paths. In this stochastic setting, second- and especially third-order labels become significantly noisier. Figure 2 shows that curvature-aware second-order supervision remains robust, consistently outperforming random-direction baselines. In contrast, naive inclusion of third-order supervision degrades performance due to noise. However, the uncertainty-based loss balancing mechanism automatically downweights unstable derivative orders (Figure 3) and restores convergence, making higher-order training robust even in noisy regimes.
Fig. 2: Test-set RMSEs over training batches for the Monte Carlo simulated Bachelier basket call. Curves show mean RMSE across 10 random seeds with shaded standard deviations. Panels show errors in the predicted values and the learned derivatives.
Fig. 3: Normalized loss weights over training for the Monte Carlo simulated Bachelier basket call.
Finally, we study computational efficiency in a 50-dimensional basket option under MC simulation, where runtime becomes the dominant constraint. As shown in Figure 4, randomized Hessian sketching delivers the best accuracyruntime trade-off, reaching target error levels significantly faster than full Hessian supervision or random-direction baselines.
Fig. 4: Test-set RMSEs over training time for the Monte Carlo simulated Bachelier basket call (basket size 50 ) with derivative labels averaging 1000 paths each. Curves show mean RMSE across 10 random seeds with shaded standard deviations. Panels show errors in the predicted values and the learned derivatives.
Across all experiments, directional Sobolev training with curvature-aware sketching improves convergence speed and final accuracy. The methods remain robust under Monte Carlo noise and scale effectively to high-dimensional pricing problems. These results demonstrate that randomized Hessian sketching enables practical higher-order training of neural surrogate models in realistic quantitative finance settings.
Implications for Quantitative Finance
From a practical standpoint, this framework enables:
- Faster surrogate model training
- More accurate Greeks
- Reduced Monte Carlo sample requirements
- Real-time pricing and risk engines
- Efficient model compression and distillation
Final Remarks
Higher-order Sobolev training contains enormous untapped potential, but computational barriers have historically limited its use. By combining algorithmic differentiation with randomized numerical linear algebra, we overcome these barriers and make second- and third-order training practical in high-dimensional settings. Directional Sobolev training via Hessian sketching provides a principled, scalable, and highly effective framework for learning accurate neural surrogates of complex financial models, enabling efficient pricing, Greeks and risk analysis.
References
This article is based on my Master’s thesis:
Efficient Higher-Order Sobolev Training via Randomized Hessian Sketching
RWTH Aachen University, 2025.