Introduction:
In the first part of this series, I discussed different preprocessing techniques for Bitcoin financial data. We built labeled pricing sequences and trained LSTM RNN moddels for short-term predictions. Next, the goal is to predict larger market movements in order to make up for trading fees. To do this, the model needs to predict further into the future and the past data it’s predictions are based on, will need to cover a longer timeframe. The naiive way to just increase the sequence length can lead to memory blow-up and long training times. Another way would be to reduce the “resolution” and have each data point in the sequence represent a longer interval. This can have the benefit of reducing noise but it can also lose important details that the model mights need for it’s predictions. A compromise might be to use non-uniform time resolution, where the resolution gets lower towards the past end of each sequence. This way, the sequences can cover a long time frame while keeping details in recent market movements intact. In this post I will be comparing these three approaches to see which one works best for this usecase.
Updated Labeling Technique:
Ground truth labeling undergoes a minor alteration. A buy/sell is now identified when there’s a price change that would make trading profitable after accounting for fees, typically around 0.15% up or down. For a large and balanced training set, I’m aiming for a distribution of 33% buys, 33% sells, and 33% holds (no action). Given the 0.15% movement threshold, this means making predictions roughly 10 hours into the future; opposed to ~90 minutes in the previous post.
Non-Uniform Time Resolution:
Standard time series data often employs fixed time intervals, such as 5-minute candles. This fixed approach provides uniformity; however, such high resolution at the past end of a sequence might not be very helpful for the prediction model. I suspect only the more significant market movements are relevant at the beginning of each sequence. By representing past data in a coarser manner and refining the granularity towards the present, it is possible to capture a more extended timeframe within each sequence – without blowing up the length of the sequence itself. This approach not only keeps sequences from becoming too large for memory, it also keeps details in the most recent market movements intact while reducing noise in the larger-scale movements of the past. This mirrors the intuitive way traders often analyze chart data.
Figure 1 gives a visusal representation of the varying resolution over the length of each sequence.
Expected Benefits of Non-Uniform Time Resolution:
Reduced Overhead: Less memory and computational resources are required as the data’s granularity varies based on its “relevance”.
Enhanced Focus: By minimizing unnecessary details and emphasizing recent market movements, non-uniform time resolution provides a clearer picture of market dynamics over extended periods.
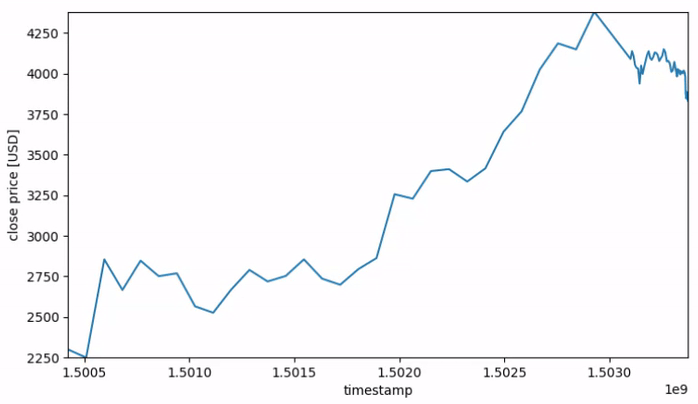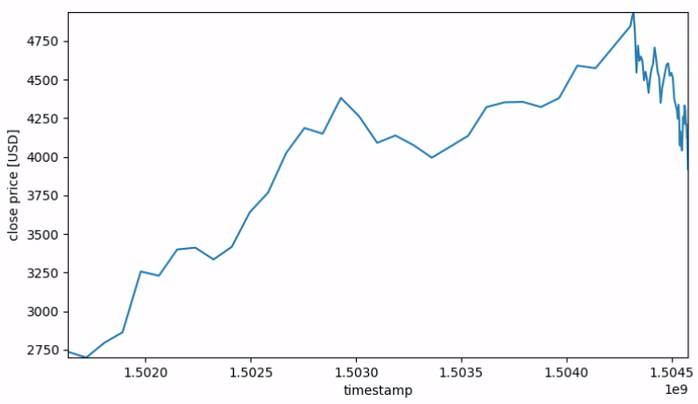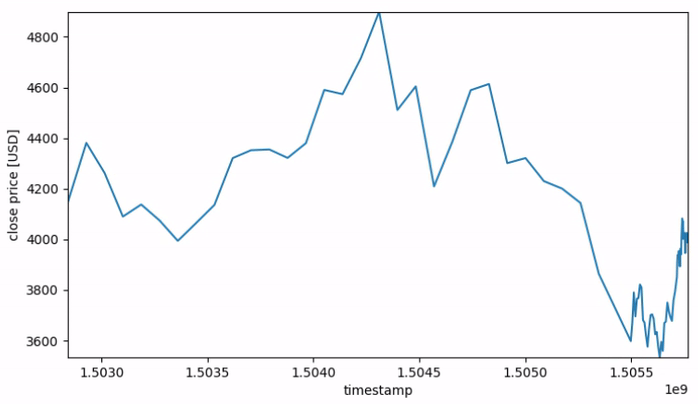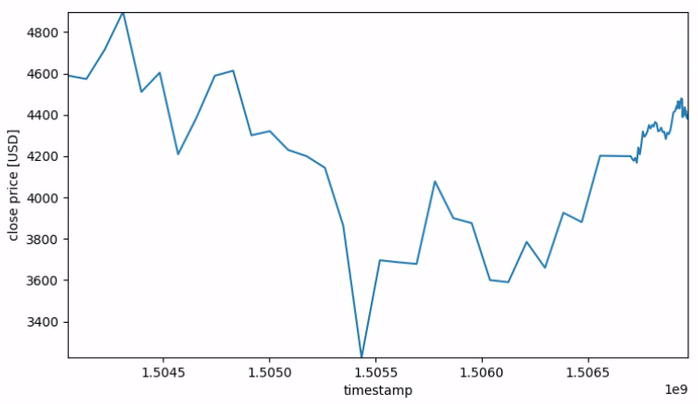
Fig. 1: Price sequences with non-uniform time resolution.
Results:
The model from the previous post serves as a baseline. The structure of the sequences is kept the same (180x 5-minute candles) and just the prediction horizon is increased. Increasing the length of the sequences from 180 to 300 candles leads to small bump in accuracy, which can be attributed to the longer context that the model can work with. Making the sequences even longer was not feasable due to memory constraints but would probably lead to diminishing improvemnts in accuracy.
To incorporate a longer time frame, I tested two more uniform approaches, one with 30-minute candles and one with 4-hour candles. Intrestingly the accuracy of the 30-minute model was worse than the baseline, while the 4-hour model achieved the overall highest accuracy. This could be attributed to the benefits of noise reduction:
- On short timeframes, financial markets can contain a lot of fluctuations that may not contribute to predictive power. These might introduce too much variance, making it harder for the model to generalize.
- A 4-hour resolution smooths out irrelevant micro-movements and focuses on meaningful trends. This leads to more stable input features, making training more effective.
The models trained on sequences with non-uniform time resolution achieved the second highest accuracy while using much shorter sequences. These results confirm the expected benefit of reducing memory and computational demands, while keeping predictive quality high. However, using uniform 4-hour candles still let to a better result. Therefore, these results can not confirm the second expected benefit of enhanced focus on relevant features. This might be due to several potential reasons:
- The model might not need much fine-grained resolution. If broader trends (multi-hour) dominate, then a non-uniform approach incorporating 30-minute candles doesn’t add much value over just using a uniformly coarser resolution.
- Using 24-hour candles leads to too much averaging. If the price moves significantly in the last 30 minutes of a candle, it gets blurred into the full period.
- With 200 × 4-hour candles, the model sees more individual observations of market structure. With a longer context, the number of effective samples is reduced, which could lead to worse learnig efficiency.
- The model might not actually need such a long context if the most useful predictive information is already captured within 200 × 4-hour candles
- The model struggles to integrate different time scales. Even if the lower resolutions contains useful long-term context, the current model might not be efficiently combining the different resolutions.
| resolution | sequence length | time frame in sequence | predicting ahead | validation accuracy |
| baseline: uniform 5 minute candles | 180 | 15 hours | 10 hours | 0.470 |
| uniform 5 minute candles | 300 | 25 hours | 10 hours | 0.473 |
| uniform 30 minute candles | 180 | 60 hours | 10 hours | 0.465 |
| non-uniform 30x 30m, 30x 2h, 30x 24h candles | 90 | 795 hours | 10 hours | 0.477 |
| uniform 4 hour candles | 200 | 800 hours | 10 hours | 0.494 |
| non-uniform 30x 4h, 30x 24h candles | 60 | 840 hours | 10 hours | 0.486 |
| non-uniform 100x 4h, 100x 24h candles | 200 | 2800 hours | 10 hours | 0.480 |
Fig. 2: Results of the comparison between differently structutred input sequences
To explore the benefits of using different time resolutions even further, it might be interesting to look at approaches that do not linearly decrease the resolution towards the past end of each sequence, but dynamically adjust it based on markers such as market volatility. Additionally, it would be intresting to try multi-branch LSTM architectures where each branch processes a different resolution seperately, before combining them to make a final prediction. This way the model could learn independently which time resolution to focus on at which point.